Intel Realsense T265 Quaternion considerations

It has taken me a while to figure out how to use the camera pose data sent from the T265.
The Intel Realsense T265 pose a combination of a quaternion and translation vector.

Lets define some things:
  Camera Pose: the location and orientation of the camera in space.  Relative to the world coordinates.

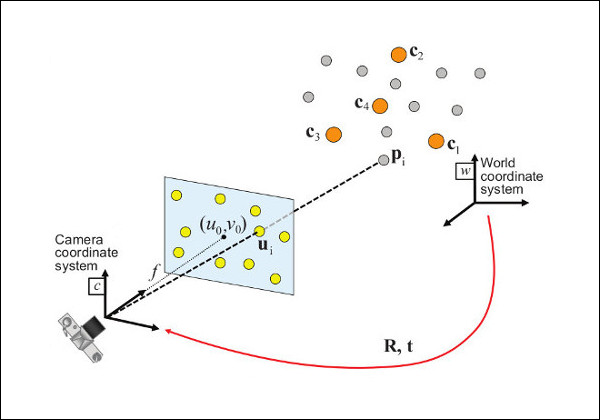https://docs.opencv.org/master/dc/d2c/tutorial_real_time_pose.html

  Quaternion: A 4D representation of 3D rotation and/or orientation.  Useful because quaternion math is faster than matrix algebra and does not have gimbal lock error.  There are multiple ways of representing a quaternion.

different ways of writing a quaternion.  Image credit Wikepedia.

All of them are derived from rotating around a vector.  (i.e. rotating theta radians around vector v)

All quaternion represntations have a real number and 3 complex number.  The real number is the cosine (rotation angle/2).  The complex values are the sine (rotation angle /2) multiplied by the vector defining the axis of rotation in x,y, and z.  The three values scale complex values i, j, and k respectively.  - Look, it's a complicated thing to get you mind around, that's why it took me about a year to understand (well.. and I ain't that smart anyhow).  It's funny, I kind of sense (or even feel) an interpretation of a matrix, but not a quaternion. I think it's the 1/2 angle that gets me.  And double coverage is weird. You can get the same rotation by going in different directions ( think -180 and 180 degrees).  Make sure you check out item #6 below for help visualizing quaternions.

  Translation vector: a 3D value representing the direction and magnitude in X, Y, Z coordinates that an object (camera) has moved.

  Rotation matrix: A 3x3 set of numbers that represents where the unit vectors for +x, +y, and +z axes will be located in world coordinates, as long as they start at the origin 0,0,0 (and have length equal to 1).

  R|t matrix: A 4 x 3 matrix made up of the Rotation matrix and the translation vector.  The camera pose can be represented as an R|t matrix.  The quaternion must be converted to the R matrix.

R|t matrix (used as camera pose matrix)

In practice,you want to turn this into a 4x4 homogeneous matrix where the
bottom row = 0 0 0 1

That allows square matrices to be multiplied together.  

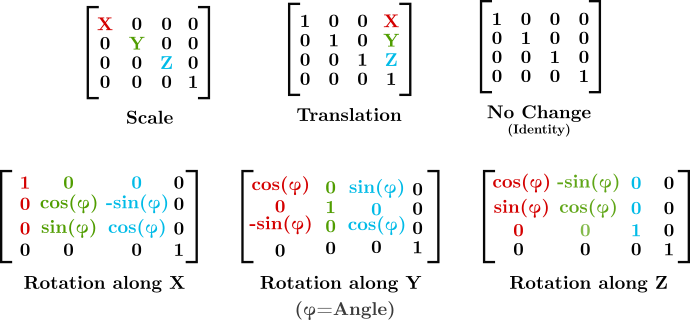Some of the types of 4x4 homogeneous matrices that can be combined by matrix multiplication.
https://sinestesia.co/blog/tutorials/python-cube-matrices/

  Essential Matrix: Not to confuse things too much, but the R|t matrix can be defined as a 3 x 3 matrix called the essential matrix. It is not used in this blog post.  I just wanted to drop a note about it.  It is typically used to find the 3D point correspondence from two camera poses.  The essential matrix associates a 2D point in an image with a line that exists in both camera images.  However, to create the essential matrix the 3 x 3 Rotation matrix is multiplied by the Skew Symmetric form of the translation vector t.  You can retrieve R and t from the essential matrix.  Check the Wikipedia page for Essential matrix.  Look at the section "Determining R and t from E".

--

I started to use the Intel Realsense cameras while at the same time learning linear algebra.  Because I didn't know about the advantages that quaternions have when interpolating movement, I continued down the matrix path.   That meant the quaternion pose data needed to be converted to a rotation matrix.  Wikipedia has an article, but I found some code examples that allowed me to convert a quaternion to a rotation matrix, and a rotation matrix to a quaternion.  There were, of course, errros.  some were mine, and some were documentation.



The key shortcuts I needed are outlined here:

1) The T265 Pose axes are not in the same orientation as the D435.

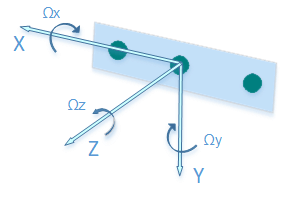D435 Pose axes

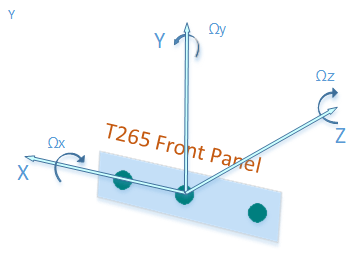T265 pose axes

T265 Z and Y axis are rotated around x axis (in relation to the D435)

D435 above a T265.  Y axis revered, Z axis revered. X axis aligned.

You need an R|t matrix to get from T265 pose data to D435 pose.


2) The Quaternion value displayed is not in the order that most quaternion explanations use.  Most use the format where the real value is on the left, followed by the i, j, k complex valued to the right of the real.  The Realsense viewer places the real value on the right.
Realsense quaternions are displayed [x,y,z,w].  The display does not label the elements.
Most formulas would be formatted as [w,x,y,z], or  a+bi+cj+dk or qr, qx,qy,qz.  In all those cases the real is on the left, complex on right. 

3)  The T265 camera orients itself to gravity.  It decides where up is, then once it has a valid pose, it projects that x and z axes on the ground plane.  That's how it defines its world coordinates.

4) If you want to convert the quaternion to a Rotation matrix take a look at this site
https://www.euclideanspace.com/maths/geometry/rotations/conversions/quaternionToMatrix/index.htm  - But caution... There are errors in thier code.

or try Quaternion Derived rotation matrix on wikipedia, its just, um, Wikipedia, so you might need a masters degree to understand it.

Here is a link to my LabView code that will convert the quaternion to a rotation matrix
https://drive.google.com/drive/folders/1rJ3j662i-Naq2tXvlYXebeRyU57GD1RZ?usp=sharing
If you use it, you to take all the blame and give me all the credit.  And if you make something that is a financial success cut me in on the money.

oh boy, math.  that's fun.

5)  It is not easy to "see" how the quaternion converts to a rotation matrix.
  Here are some quaternion to rotation matrix examples

6) Have a look at the 3 blue one brown collaboration with eater.net to Visualize Quaternions
It is the most helpful thing on the internet regarding quaternions.